Question

Determine the initial concentration of hypochlorous acid that would result in a solution with a pH of 3.2Ka = 3.0 x 10^-8

Answer 1

To answer this question, we will need to use an ICE table.

So, we start with the concentration we want to calculate, [HClO].

The dissociation equilibrium is:

`HClO\rightleftarrows H^++ClO^-`

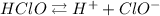
At start, we only have HClO, so the first row of the table is:

HClO | H⁺ | ClO⁻

[HClO]i | 0 | 0

Now, suppose x dissociates at the equilibrium, so we would have:

HClO | H⁺ | ClO⁻

[HClO]i | 0 | 0

[HClO]i - x | x | x

Since the concentration of H⁺ will be x, we can calculate it by using the given pH:

`\begin{gathered} pH=-\log \lbrack H^+\rbrack \\ x=\lbrack H^+\rbrack=10^(-pH)=10^(-3.2)\approx6.30957*10^(-4)M \end{gathered}`

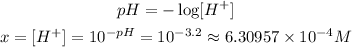
Now, we can figure the initial concentration of HClO by using the equilibrium equation:

`Ka=(\lbrack H^+\rbrack\lbrack ClO^-\rbrack)/(\lbrack HClO\rbrack)`

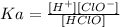
From the ICE table, we have:

`\begin{gathered} \lbrack H^+\rbrack=x\approx6.30957*10^(-4)M \\ \lbrack ClO^-\rbrack=x\approx6.30957*10^(-4)M \\ \lbrack HClO\rbrack=\lbrack HClO\rbrack_i-x=\lbrack HClO\rbrack_i-6.30957*10^(-4)M \end{gathered}`

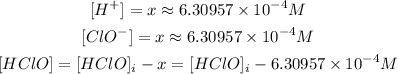
Thus:

`3.0*10^(-8)=(6.30957*10^(-4)M\cdot6.30957*10^(-4)M)/(\lbrack HClO\rbrack_i-6.30957*10^(-4)M)`

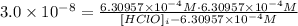
Now, we can solve for [HClO]i:

`\begin{gathered} 3.0*10^(-8)=(6.30957*10^(-4)M\cdot6.30957*10^(-4)M)/(\lbrack HClO\rbrack_i-6.30957*10^(-4)M) \\ 3.0*10^(-8)(\lbrack HClO\rbrack_i-6.30957*10^(-4)M)=3.98107*10^(-7)M \\ 3.0*10^(-8)\lbrack HClO\rbrack_i-1.89287*10^(-11)=3.98107*10^(-7)M \\ 3.0*10^(-8)\lbrack HClO\rbrack_i=3.98107*10^(-7)M+1.89287*10^(-11)M \\ 3.0*10^(-8)\lbrack HClO\rbrack_i=3.98126*10^(-7)M \\ \lbrack HClO\rbrack_i=(3.98126*10^(-7)M)/(3.0*10^(-8)) \\ \lbrack HClO\rbrack_i\approx0.1327M \end{gathered}`

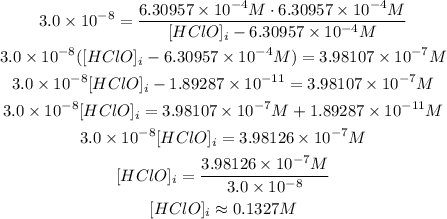
Thus, the initial concentration is approximately 0.1327 M.