We are given that a pyramid has a height of 25 cm and the base has dimensions of 6cm by 10 cm. To determine its volume we will use the following formula:
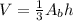
Where:
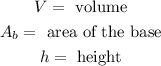
To determine the area of the base we use the area of a rectangle, which is the product of its dimensions:
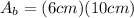
Solving the operations:
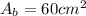
Now, we plug in the values in the formula for the volume:
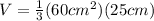
Now, we solve the operations:
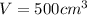
Therefore, the volume is 500 cubic centimeters.