Question

The measure of one angle of a right triangle is 32∘ more than the measure of the smallest angle. Find the measure of the smallest angle.

Answer 1

To find the measure of the smallest angle, you can follow the steps.

Step 1: Organize your information.

Let's suppose you have angles A, B, and C.

Since it is a right triangle, one angle is equal to 90°.

So, A = 90 °.

Also,

The measure of one angle is 32 more than the measure of the smallest angle.

Let B be the smallest angle, and C be B + 32°.

Let's say B measures x.

Then,

A = 90

B = x

C = x + 32

Step 2: Sum the angles.

The sum of the interior angles of a triangle is 180°. So,

`A+B+C=180`

And, substituting the values:

`90+x+x+32=180`

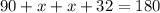
Adding similar terms:

`122+2x=180`

Step 3: Isolate x.

To do it, first, subtract 122 from each side.

`\begin{gathered} 2x+122-122=180-122 \\ 2x=58 \end{gathered}`

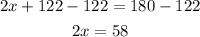
Now divide both sides by 2.

`\begin{gathered} (2x)/(2)=(58)/(2) \\ x=29 \end{gathered}`

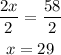
Since x is the measure of B, and B is the smallest angle, the measure of the smallest angle is 29°.

Answer: 29°.