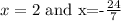Question

Find the solution for x if |7x + 5|= 19. Where | | denotes the absolute value

Answer 1

We have the following expression:

`|7x+5|=19`

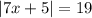
where the bars | | denote the absolute value.

This absolute value equation implies that we have 2 cases:

`\begin{gathered} \text{case A) 7x+5=19} \\ \text{case B) 7x+5=-19} \end{gathered}`

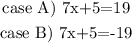
Case A)

In this case, if we move +5 to the right hand side, we get

`\begin{gathered} 7x=19-5 \\ 7x=14 \end{gathered}`

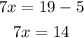
Now, if the move the coefficient of x to the right hand side, we have

`\begin{gathered} x=(14)/(7) \\ x=2 \end{gathered}`

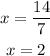
that is, the solution for this case is x=2

Case B).

In this case, if we move +5 to the right hand side, we obtain

`\begin{gathered} 7x=-19-5 \\ 7x=-24 \end{gathered}`

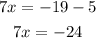
Finally, f the move the coefficient of x to the right hand side, we get

`\begin{gathered} x=-(24)/(7) \\ \end{gathered}`

that is, the solution for this case is x=-24/7

Therefore, the solution for the problem is

`x=2\text{ and x=-}(24)/(7)`