Question

Three thousand dollars is left in a bank savings account drawing interest compounded quarterly at 5%. How long will it take for the balance triple?

Answer 1

22 years

Step-by-step explanation

The balance in a savings account with compound interest is,

`A=P\mleft(1+(r)/(n)\mright)^(nt)`

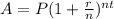
Where:

• P is the principal amount

,

• r is the interest rate

,

• n is the number of times the interest is compounded per year

,

• t is the time in years

,

• A is the balance in the account after t years

In this case, we have that the interest rate is r = 0.05, the interest is compounded quarterly so n = 4, and we have to find t for A = 3P,

`3P=P\mleft(1+(0.05)/(4)\mright)^(4t)`

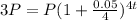
To solve, divide both sides by P,

`\begin{gathered} 3=\mleft(1+0.0125\mright)^(4t) \\ 3=(1.0125)^(4t) \end{gathered}`

Then, take the logarithm to both sides of the equation. This way we apply the property of the logarithm of a power,

`\begin{gathered} \log 3=\log (1.0125^(4t)) \\ \log 3=4t\log (1.0125) \end{gathered}`

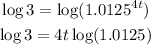
Divide both sides by 4*log(1.0125) and solve,

`t=(\log 3)/(4\log (1.0125))\approx22.11`

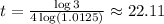
Hence, it will take approximately 22 years for the balance to triple.