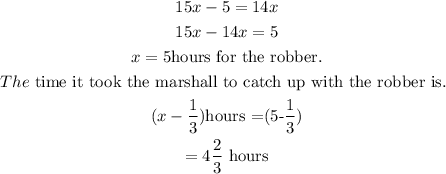After robbing a bank in Dodge City a robber gallops off at 14 mi/h. 20 minutes later, the marshalls leaves to pursue the robber at 15 mi/h. How long (in hours) does it take the marshalls to catch up to the robber?
SOLUTION
Let it take x hours for the marshall to catch up with the robber since the robber started galloping.
In x hours, the robber would have covered 14 x miles
Now, the time for the marshall to catch the robber would be x - 20 minutes
=
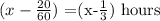
The distance the marshall would have covered is.
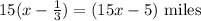
This distance is equal, so