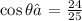Given the following:
a.) tan θ = 7/24
Let's make a graph to better understand the problem,
SOLUTION 1:
Let's first recall the function of Tan θ and Cos θ,
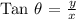
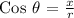
From the given function, it appears that x = 24 and y = 7. To be able to determine the value of Cos θ, we must first determine the value of r using the Pythagorean Theorem:
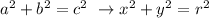
![r\text{ = }\sqrt[]{x^2+y^2}](https://img.qammunity.org/2023/formulas/mathematics/college/bmxx0q75bc2y12ia1h79lss2wzm9328qrv.png)
![\text{ = }\sqrt[]{24^2+7^2}\text{ = }\sqrt[]{576\text{ + 49}}](https://img.qammunity.org/2023/formulas/mathematics/college/x7yg129z07nexx11qrb4cacda3ryb0razl.png)
![\text{ = }\sqrt[]{625}](https://img.qammunity.org/2023/formulas/mathematics/college/6u0u2v9kiftct9rktlx71sl0c4he3fi4gw.png)

Let's find the value of Cos θ,
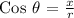
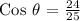
Therefore, the value of Cost θ is 24/25.
SOLUTION 2:
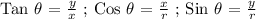
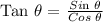
Since y = 7 and x = 24, we get:
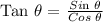

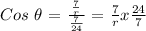
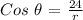
From the given graph, we found out that r = 25 after applying the Pythagorean Theorem. Therefore, to complete the value of cos θ,
we substitute r = 25.
Therefore,