Let's take the origin where the first friend began. Since this friend started walking with a constant speed of 0.5 m/s and is walking towards the friend (that we are going to assume is to the right) we have that its position at any given time is:
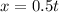
The position of the second friend starts at 50 m to the right and its motion is to the left, since it is walking with costant acceleration its position at any given time is:
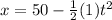
to determine how long it takes for them to meet we equate the positions and solve for t:
![\begin{gathered} 0.5t=50-(1)/(2)(1)t^2 \\ t=100-t^2 \\ t^2+t-100=0 \\ t=\frac{-1\pm\sqrt[]{1^2-4(1)(-100)}}{2(1)} \\ t=\frac{-1\pm\sqrt[]{401}}{2} \\ \text{then} \\ t=\frac{-1+\sqrt[]{401}}{2}=9.51 \\ \text{ or} \\ t=\frac{-1-\sqrt[]{401}}{2}=-10.51 \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/hcoj0pycp9o1lrd61fwlygfg7gwvxkxcwi.png)
Since time has to be positive we choose the positive solution for the equation.
Theredore, we conclude that it took 9.51 s for the friends to meet.