Question

Find the length of the side labeled x. Round intermediate values to the nearest tenth. Use the rounded values to calculate the next value. Round your final answer to the nearest tenth.A. 20.9B. 23.6C. 31.1D. 31.6

Answer 1

hello

to solve this problem, we would have to find the adjacent side of the bigger triangle using trigonometric ratios

using SOHCAHTOA

`\begin{gathered} \tan \theta=(opposite)/(adjacent) \\ \theta=58^0 \\ \text{opposite}=29 \\ \text{adjacent}=y \\ \tan 58=(29)/(y) \\ y=(29)/(\tan 58) \\ y=18.12 \end{gathered}`

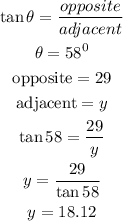
with the value of adjacent, we can as well assume it is the value of the opposite side of the smaller triangle.

to find the value of x, let's use the sine angle of this

`\begin{gathered} \sin \theta=(opposite)/(hypothenus) \\ \sin 29=(18.12)/(x) \\ x=(18.13)/(\sin 50) \\ x=23.6 \end{gathered}`

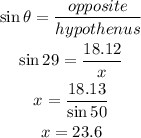
from the calculations above, the value of x is equal to 23.6 which corresponds to option B