Question

I don't understand can u put 6 statements and reasons

Answer 1

Statement 1:

`\bar{JN}\cong\bar{NL},\angle JMK\cong\angle LKM`

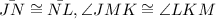
Reason 1:

Given

Statement 2:

`\bar{JK}\parallel\bar{ML}`

Reason 2:

Alternate interior angles converse theorem

(this means that the only way that this two angles would be equal is that the lines stated above are parallel)

Statement 3:

`\angle JKM\cong\angle LMK`

Reason 3:

Alternate interior angles theorem.

(this means that once we proved that segments JK and ML are parallel the alternate interior angles should be equal)

Statement 4:

`\bar{MN}\cong\bar{MN}`

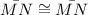
Reason 4:

Reflexive property of congurence

Statement 5:

`\Delta JMK\cong\Delta LKM`

Reason 5:

ASA

(this means that two triangles are congruent is the angle side angle are conguent)

Statement 6:

JKLM is a parallelogram

Reason 6:

The diagonal MK divides the quadrialteral in two congruent triangl