Question

Hello, I need help with this precalculus homework question, please?HW Q7

Answer 1

1) Note that since we cannot reduce both sides of that equality to the same base, one way to rewrite it is to resort to a logarithm.

The Definition of a Logarithm is:

`\log_ab=c\Leftrightarrow a^c=b`

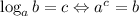
2) Now, we can rewrite that exponential statement as a logarithm that way:

`\begin{gathered} a^7=5.8 \\ \log_aa^7=\log_a5.8 \\ \log_a5.8=7\Leftrightarrow a^7=5.8 \\ \log_a5.8=7 \end{gathered}`

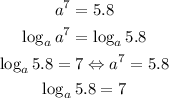
Note that whenever the base of a logarithm is the same as the exponent of its argument we can tell that log is equal to its exponent.