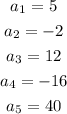Answer
Step-by-step explanation
Given:
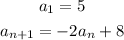
To determine the first five terms of the given recursive defined sequence, we follow the process as shown below:
The first term is given, so:
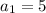
Next, we plug in n=1 and a1=5 into the given formula to get the second term:
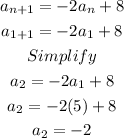
Hence,
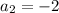
We plug in n=2 and a2=-2:
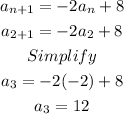
We plug in n=3 and a3=12 into the given formula:
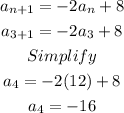
Then, we plug in n=4 and a4=-16:
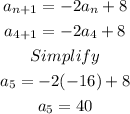
Therefore, the answers are: