The first step to solve the system of equation is to solve one of the equations for one variable:
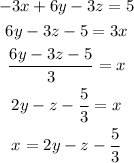
Replace this variable for the obtained expression in the other two equations:
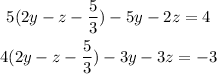
Now, solve the system just as if it were a 2x2 system:
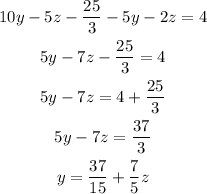
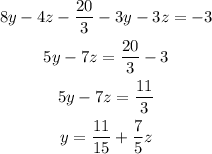
Make both expressions for y equal and solve for z:
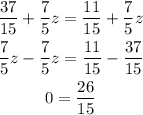
Since 0 is not equal to 26/15, we can determine that this system does not have any solution.
The correct answer is No solution.