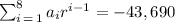Question

Write the sum using sigma notation: −2 −8 −32 +... −32768∑i=1

Answer 1

Given

-2-8-32+...-32768

Find

Write the sum using the sigma notation

Step-by-step explanation

we have given - 2 - 8 - 32 + ... - 32768

here a = -2

common ratio = -8/-2 = 4

nth term = -32768

now from the nth term formula we find the number of terms

`\begin{gathered} a_n=ar^(n-1) \\ -32768=-2(4)^(n-1) \\ 16384=(4)^(n-1) \\ 4^7=(4)^(n-1) \\ 7=n-1 \\ n=8 \end{gathered}`

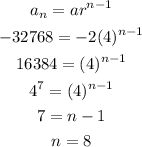
so , sum =

`\sum_{i\mathop{=}1}^8a_ir^(i-1)=a_1r^(1-1)+a_2r^(2-1)+a_3r^(3-1)+.........+a_8r^(8-1)`

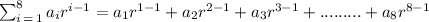
sum of geometric progression is given by

`\begin{gathered} S_8=(a(r^n-1))/(r-1) \\ \\ S_8=(-2(4^8-1))/(8-1) \\ \\ S_8=(-2(32768-1))/(7) \\ S_8=-43,690 \\ \end{gathered}`

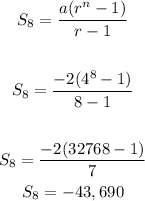
Final Answer

`\sum_{i\mathop{=}1}^8a_ir^(i-1)=-43,690`