The slope (m) of the hypotenuse of a triangle is defined by the relation:
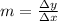
Where Δy is the length of the vertical side of the triangle, and Δx is the length of the horizontal side of the triangle.
We are told to prove that the hypotenuse of both triangles have the same slope, to do this, First, let's find the slope of the line AB (m(AB)) applying the above formula
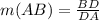
And now, let's find the slope of the line AC (m(AC))
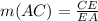
Then, when we say that both lines have the same slope, we say that m(AB)=m(AC),
And replacing m(AC) and m(AB), we can get to:
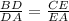
And that's the most appropriate ratio to prove that both lines have the same slope