Trigonometric Ratios
The trigonometric ratios stand in every right triangle, i.e. those triangles having one angle of 90°.
The triangle provided in the figure is right because it has a clearly marked angle of 90°. The side opposite to this angle is called the hypotenuse, and the other two sides are called the legs.
We are given the hypotenuse of AC=3.6 units, and the angle C = 70°.
To find the length of the side x, we should use a trigonometric ratio that relates the opposite side of 70° and the hypotenuse.
This ratio is called the sine, defined as follows:
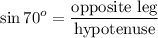
Substituting:
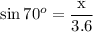
Solving for x:
x = 3.6 sin 70° = 3.6 * 0.9397 = 3.4
x = 3.4 units