Question

Consider the following parametric equations:x = -3(t – 2) and y = -3tStep 1 of 2: Eliminate the parameter 1. Please write your answer in simplest form solved for y.

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the given parametric equations

`\begin{gathered} x=-3(t-2)---equation\text{ 1} \\ y=-3t------equation\text{ 2} \end{gathered}`

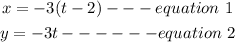
STEP 2: Rewrite equation 1

`\begin{gathered} x=-3t+6 \\ -3t+6=x \end{gathered}`

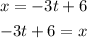
STEP 3: Make t the subject of the equation

`\begin{gathered} Subtract\text{ 6 from both sides} \\ -3t+6-6=x-6 \\ -3t=x-6 \\ Divide\text{ both sides by -3} \\ t=(x-6)/(-3) \\ t=(-(x-6))/(3)=(-x+6)/(3) \end{gathered}`

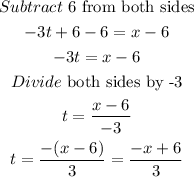
STEP 4: Substitute the value of t above into equation 2 and solve in terms of x

`\begin{gathered} y=-3t \\ By\text{ substitution,} \\ y=-3((-x+6)/(3)) \\ Cross-cancel\text{ the common factor: 3} \\ y=-(-x+6) \\ y=x-6 \end{gathered}`

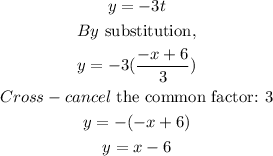
Hence, the answer in the simplest form solved for y is given as:

`y=x-6`