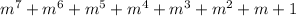We are given the following division problem
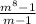
We need to factor out the numerator first
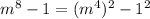
Apply the difference of squares formula
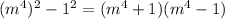
Again, factor out the term on the right side
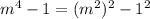
Apply the difference of squares formula
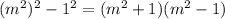
Again, factor out the term on the right side
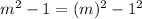
Apply the difference of squares formula
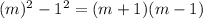
Finally, the expression becomes
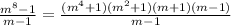
(m-1) cancels out
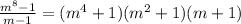
Therefore, the quotient is
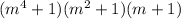
Or in simplified form