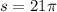We are asked to find the arc length of a segment of a circle, to do that let's remember the formula for the arclength of a circle:
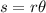
Where the greek letter theta represents the angle in radians. Since we are given the angle in degrees we need to transform it using the following relationship:
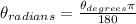
Replacing the value of theta we get:
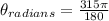
Simplifying we get:
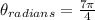
Replacing in the formula for the arc length:
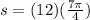
simplifying: