we have the system of equations
4x+3y=0
x+2y=5
Convert to matrix form
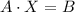
matrix A
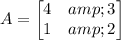
matrix X
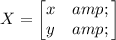
matrix B
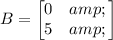
substitute
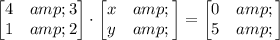
Find out the determinant of matrix A
D=4*2-3*1
D=5
Find out the determinant Dx
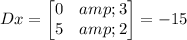
Find out the determinant Dy
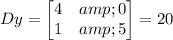
Find out the value of x
x=Dx/D
x=-15/5=-3
Find out the value of y
y=Dy/D
y=20/5=4
therefore
The solution is (-3,4)