Question

How can the graph of f(x) = 5(x+5) - 3 be obtained from the graph of y = x??

Answer 1

Shift horizontally 5 units to the left, shrink it vertically by a factor of 1/2, shift it 3 units down.

Step-by-step explanation:

Given the function;

`\begin{gathered} f(x)=(1)/(2)(x+5)^2-3\text{ ------1} \\ \text{and} \\ y=x^2\text{ --------2} \end{gathered}`

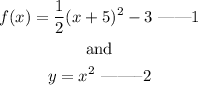
We want to determine how to derive the graph of equation 1 from equation 2.

Firstly, 5 units to the left will give;

`y=(x+5)^2`

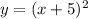
followed by a vertical shrink of factor 1/2 to give;

`y=(1)/(2)(x+5)^2`

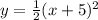
Then lastly, 3 units down to give;

`y=(1)/(2)(x+5)^2-3`

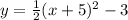
Therefore, the change is;

Shift horizontally 5 units to the left, shrink it vertically by a factor of 1/2, shift it 3 units down.