Question

Find the value of Qin the following system so that the solution to the system is {(1;y) : x – 3y=4} x – 3y=4 2x – 6y=Q

Answer 1

The solution of the system is-

`\mleft\lbrace(1;y)\colon x-3y=4\mright\rbrace`

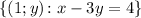
Notice that we have to find a value for Q where the given solution is valid.

Also, notice that the equation which contains to is double than the given solution. So, let's just multiply by 2 the given solution.

`\begin{gathered} 2(x-3y)=4\cdot2 \\ 2x-6y=8 \end{gathered}`

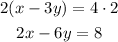
As you can observe, using the given solution to the system, Q must be equal to 8 since that's the case when the solution is valid.

Therefore, Q = 8.