Question

The permeter is 40 How much bigger is the longest side than the shortest side? 2

Answer 1

The perimeter of the triangle is the distance around it.

In the case of our triangle, the distance around it is

`(2a-3)+(3a+1)+2a`

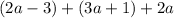
which we are told is 40 units; therefore,

`(2a-3)+(3a+1)+2a=40`

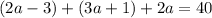
Simplifying the expression on the left side of the equation (adding like terms) gives us

`7a-2=40`

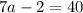
Now we solve for a by adding 2 to both sides of the equation and then dividing by 7:

`7a=40+2`
`a=(42)/(7)`
`\textcolor{#FF7968}{\therefore a=6.}`

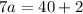
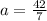
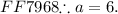
Now we are in a position to compute the length of the longest side.

The longest side is 3a+1 and it evaluates to

`3a+1=3(6)+1=19.`

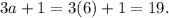
The longest side is 19 units.

The shortest side is 2a-3 and it evaluates to

`2a-3=2(6)-3=9`

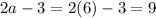
The shortest side is 9 units.

Therefore, the difference of length between the longest side and the shortest side is

`19-9=10`

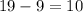
Hence, the longest side is 10 units bigger than the shortest side.