Let x, y represent the distance travelled by the cars after time, t.
We can construct a triangle for the movement of the two(2) cars, as shown below;
Let S be the distance between the two(2) cars.
By applying the Pythagoras theorem here, we have:
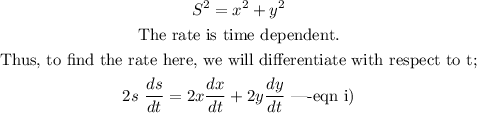

Thus, we have:
![\begin{gathered} S^2=\sqrt[]{40^2+20^2} \\ S^2=\sqrt[]{1600+400} \\ S^2=\sqrt[]{2000} \\ S=44.72 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/5x9ev8sl3mln9wq6z924qxi6e0oqcypc76.png)
For the rate of distance, we have:

Hence, the distance between the two(2) cars is changing at the rate of 89.44 miles per hour.