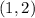Question

=Solve this system of equations byusing the elimination method.x + 4y = 92x – 4y = -6([?],[]=The ordered pair of solutionsis written in the format (x, y).

Answer 1

Given

The system of equations are

`\begin{gathered} x+4y=9.............1 \\ 2x-4y=-6...........2 \end{gathered}`

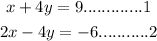
Step-by-step explanation

To find the values of x and y use the elimination method.

Add equation 1 and 2 ,

`\begin{gathered} (x+4y-9)+(2x-4y+6)=0 \\ 3x-3=0 \\ x=1 \end{gathered}`

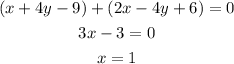
Substitute the value of x in equation 1,

`\begin{gathered} 1+4y=9 \\ 4y=8 \\ y=2 \end{gathered}`

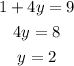
The value of x is 1 and y is 2.

Answer

The ordered pair of solutions is

x=1 and y=2.

`(1,2)`