Given:
Vertex at (-1,-2)
Goes through point (0,1)
The vertex form of a quadratic equation is defined as
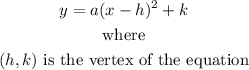
Substitute (h,k) with the vertex (-1,-2)

Now we solve for a, by substituting (x,y) with (0,1) to the vertex form of the previous equation.
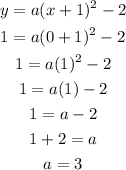
Putting it together with the vertex form we have
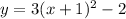
Expand the equation, and change it into standard form
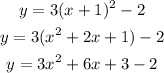
Simplify further, and the equation of the parabola in standard form is
