Question

Let f(x)=5x^3-1 and g(x)=5-4x^2. Evaluate the following. 1. f(x+2)2. (fg)(3)3. (f・f)(2)(Number 4 is a fraction)4. G(x+h)-g(x)/h Show work please!!

Answer 1

Given the functions:

`\begin{gathered} f(x)=5x^3-1 \\ g(x)=5-4x^2 \end{gathered}`

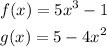
We will find the following:

First, f(x+2)

So, we will substitute with (x+2) into the function f(x)

`f(x+2)=5(x+2)^3-1`

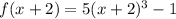
Second, (fg)(3)

so, we will find the product of the functions (f) and (g)

`(fg)(x)=(5x^3-1)\cdot(5-4x^2)`

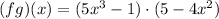
Then, substitute with x = 3

`(fg)(3)=(5\cdot3^3-1)\cdot(5-4\cdot3^2)=134\cdot(-31)=-4154`

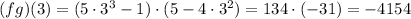
Third, (f・f)(2)

So, we will find the product of the function (f) by (f)

`\begin{gathered} (f\cdot f)(x)=(5x^3-1)\cdot(5x^3-1) \\ (f\cdot f)(x)=(5x^3-1)^2 \end{gathered}`

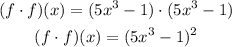
Then, substitute with x = 2

`(f\cdot f)(2)=(5\cdot2^3-1)^2=(39)^2=1521`

Finally, we will find g(x+h)-g(x)/h

So, we will find g(x+h), then substitute it into the formula.

`g(x+h)=5-4(x+h)^2`

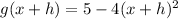
So,

`(g(x+h)-g(x))/(h)=(\lbrack5-4(x+h)^2\rbrack-\lbrack5-4x^2\rbrack)/(h)`

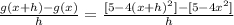
Expand the numerator then simplify the answer:

`\begin{gathered} (g(x+h)-g(x))/(h)=((5-4(x^2+2xh+h^2))-(5-4x^2))/(h) \\ \\ =(5-4x^2-8xh-4h^2-5+4x^2)/(h) \\ \\ =((5-5)+(-4x^2+4x^2)-8xh-4h^2)/(h) \\ \\ =(-8xh-4h^2)/(h)=(h(-8x-4h))/(h) \\ \\ =-8x-4h \end{gathered}`

So, the answer will be (-8x - 4h)