Given: Graph of a function is given.
Required: To identify which equation would have real zero(s) corresponding to the x-intercept(s) of the graph.
Step-by-step explanation: A function's zero(s) are represented on the graph as the x-intercept. Hence we need to solve the given equations for zero(s).
We put the equation equal to zero to solve for zero(s).
The first equation given is

Putting the equation, y=0 gives
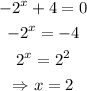
The second equation given has no x-intercept.
The third equation has an x-intercept at
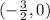
The last equation has an x-intercept at

Final Answer: Option A is correct.