Question

A child of mass 50 kg runs with a speed 0.6 m/s toward a stationary sled of mass 10 kg. The child jumps onto the sled, which slides across the snow with negligible friction.(a) What is the speed of the child-sled system after the child lands on the sled?(b) What is the kinetic energy of the child-sled system at this time?The child jumps backward off of the sled so that the child lands on the snow at rest.(c) What is the speed of the sled after the child lands?(d) What is the sled's kinetic energy after the child lands?

Answer 1

After the child lands on the sled, the child-sled system will have a speed of 0 m/s because the total momentum before and after the child lands must be zero. The kinetic energy of the child-sled system at this time is also zero because the velocity is zero. After the child jumps off the sled, the sled will have a speed of 0 m/s. The kinetic energy of the sled after the child lands is also zero.

Step-by-step explanation:

(a) To find the speed of the child-sled system after the child lands on the sled, we can use the principle of conservation of momentum. The momentum before the child jumps onto the sled is given by the product of the mass of the child and the speed of the child. Similarly, the momentum of the sled before the child jumps on is given by the product of the mass of the sled and its initial speed, which is zero. The total momentum before the child jumps on is therefore zero. After the child lands on the sled, the total momentum of the system must still be zero. So, the momentum of the child-sled system after the child lands on the sled is also zero. Since momentum is mass times velocity, we have:

1. Mass of child x Velocity of child + Mass of sled x Velocity of sled = 0
2. 50 kg x 0.6 m/s + 10 kg x 0 = 0
3. 30 kg m/s + 0 = 0
4. 30 kg m/s = 0
5. Velocity of child-sled system = 0 m/s

(b) To find the kinetic energy of the child-sled system at this time, we can use the formula for kinetic energy, which is given by half the mass times the square of the velocity. Since the velocity of the child-sled system is zero, the kinetic energy of the system is also zero.

(c) When the child jumps backward off of the sled, the total momentum of the system is still zero. So, the momentum of the sled after the child lands is also zero. Since momentum is mass times velocity, we have:

1. Mass of child x Velocity of child + Mass of sled x Velocity of sled = 0
2. 50 kg x 0 + 10 kg x Velocity of sled = 0
3. 0 + 10 kg x Velocity of sled = 0
4. Velocity of sled = 0

(d) Since the velocity of the sled is zero, the kinetic energy of the sled after the child lands is also zero.

Answer 2

Consider the law of conservation of momentum in the given situation.

(a) The momentum po of the system before the child jumps to the sled is equal to the total momentum after pf. Then, you have:

po = pf

po = m1*v1

pf = (m1 + m2)*v

where,

m1: mass of the child = 50kg

m2: mass of the sled = 10kg

v1: speed of the child = 0.6m/s

v: speed of the child and the sled togueter = ?

Solve the equation above for v and replace the previous values of the parameters:

The speed of the system child-sled is 0.5m/s

(b) The kinetic energy is given by:

`\begin{gathered} K=(1)/(2)(m_1+m_2)v^2 \\ K=(1)/(2)(50kg+10kg)(0.5(m)/(s))^2 \\ K=7.5J \end{gathered}`

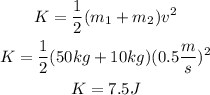
The kinetic energy of the child-system is 7.5J

(c) Again, the total momentum must conserve before and after the child jumps backward off the sled. If after the jump the child is at rest on the snow, you have:

po = pf

po = (m1 + v1)*v

pf = m2*v2

where,

v2: speed of the sled after the child jumps backward off the sled = ?

equal the expressions for po and pf, solve for v2 and replace the values of the rest of the paramters:

After the child lands the speed of the sled is 3m/s

(d) The kinetic energy is given by:

`\begin{gathered} K=(1)/(2)m_2v^2_2 \\ K=(1)/(2)(10kg)(3(m)/(s))^2 \\ K=45J \end{gathered}`

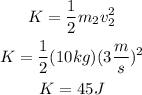
The kinetic energy of the sled is 45J