Question

A species of beetles grows 39% every year. Suppose 100 beetles are released into a field.Construct an exponential model for this population.How many beetles will there be in 10 years?How many beetles will there be in 15 years?About when will there be 100,000 beetles?

Answer 1

As suggested, first, we will construct a model and then we will evaluate it at t=10, t=15, and finally, we will set the equation equal to 100,000 and solve for t.

The species grows 39% every year, therefore, if T is the total number of beetles, we can set the following equation:

`T=100(1+0.39)^t.`

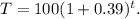
Evaluating the above equation at t=10, we get:

`T=100(1.39)^(10)=2692.452204\approx2692.`

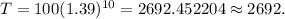
Evaluating the above equation at t=15, we get:

`T=100(1.39)^(15)=13970.82343\approx13971.`

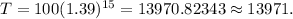
Note that I rounded to the nearest integer because you cannot have a piece of beetle.

Now, setting T=100,000 and solving for t, we get:

`\begin{gathered} 100,000=100(1.39)^t, \\ 1000=1.39^t, \\ \log 1000=t\log 1.39, \\ t=(\log 1000)/(\log 1.39)=(3)/(\log 39)\approx21. \end{gathered}`

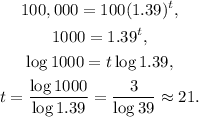
Answer:

After 10 years there will be 2692 beetles.

After 15 years there will be 13971 beetles.

About 21 years later there will be 100,000 beetles.