(1) Angle 6 and angle 7 lie on a straight line. Therefore
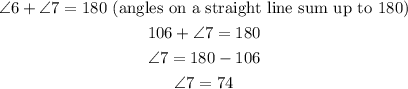
(2) If angle 6 equals 106, then angle 4 corresponds to angle 6. Therefore angle 4 equals 106. Angle 1 and angle 4 lie on a straight line. Therefore;
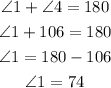
(3) Angle 3 is vertically opposite to angle 4
(4) Angle 8 is vertically opposite to angle 7
(5) Angles 1 and 3 are NOT CONGRUENT to each other
(6) Angles 2 and 7 are CONGRUENT to each other. Interior alternate angles are equal. Angles 2 and 7 are interior alternate angles
(7) Lines a and b are PARALLEL
(8) Line t is a TRANSVERSAL