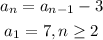Question

PLEASE HELP PLEASE Write a recursive sequence that represents the sequence defined by thefollowing explicit formula:a_n = 7-3(n-1)

Answer 1

`\begin{gathered} a_n=a_(n-1)-3 \\ a_1=7,n\geq2 \end{gathered}`

Explanation:

Given the explicit formula of the sequence:

`a_n=7-3(n-1)`

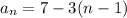
First, find the first three terms of the sequence:

`\begin{gathered} a_1=7-3(1-1)=7-3(0)=7 \\ a_2=7-3(2-1)=7-3(1)=4 \\ a_3=7-3(3-1)=7-3(2)=1 \end{gathered}`

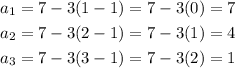
From the first third terms, we see that to obtain the next term, we subtract 3 from the previous term. That is:

`a_n=a_(n-1)-3`

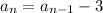
Therefore, the recursive sequence is:

`\begin{gathered} a_n=a_(n-1)-3 \\ a_1=7,n\geq2 \end{gathered}`