Question

The population of Maxville in 2005 was 13,625 people. In 2009 the population had grown to 15,325 people. Assume that thepopulation growth is linear, and 2000.(a) Write a function for the population, p, interms of the number of years since 2000, t(b) Identify the slope of the function and explain its practical meaning in the context of the problem. Include unitsc) identify the vertical intercept (y intercept)of the function & explain meaning. include unitsd) use function from part A to estimate population in 2015e) when will the population reach 20,425

Answer 1

So, to find the linear function that we're asking for, we should find the slope first: (Notice that the independent variable t, is taken as the number of years since 2000, so we're going to take 9-5 instead of 2009-2005).

`m=(15325-13625)/(9-5)=425`

Now that we know that the slope is 425, we could replace a point in the general form of a linear function:

`y=mx+b`

Where m is the slope and b is the y-intercept. Let's replace the pair (5, 13625) to find the value of b.

`\begin{gathered} 13625=425(5)+b \\ b=13625-2125 \\ b=11500 \end{gathered}`

Therefore, the equation of the linear function is:

`p(t)=425t+11500`

b. The slope of the function is 425. It represent that the population increases 425 people each year.

c. The vertical intercept of the function is y=11,500. It represents that in the year 2000, there were 11,500 people in Nashville.

d. To estimate the population in 2015, we replace t=15:

`\begin{gathered} p(15)=425(15)+11500 \\ p(15)=17875 \end{gathered}`

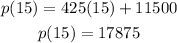
Therefore, there would be 17875 people in 2015.

e. To find the time t when the population will reach 20,425 people, we replace p by 20,425 and then solve this equation for t:

`\begin{gathered} 20425=425t+11500 \\ 20425-11500=425t \\ 8925=425t \\ t=21 \end{gathered}`

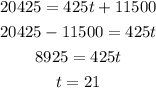
Therefore, the population will reach 20,425 in the year 2021.