Question

A game is played with a single fair die. A player wins $20 if a 2 turns up, $40 if a 4 turns up, and loses $30 if a 6 turns up. If any other face turns up, there is no winning. Find the expected sum of money the player can win.$3$4$5$6.50

Answer 1

Given that a game is played with a single fair die. A player wins $20 if a 2 turns up, $40 if a 4 turns up, and loses $30 if a 6 turns up. If any other face turns up, there is no winning

To Determine: The expected sum of money the player can win

Solution:

Let X be the the random variable giving the amount of money won on any toss of the die

The possible amounts won when the die turns up 1,2, 3, 4, 5, and 6 are:

X1, X2, X3, X4, X5, and X6 respectively.

While the probabilities of these are P(X1), P(X2), P(X3), P(X4), P(X5), and P(X6).

Note that the probability of any face turning up in a fair die is

`P(a\text{ face turn up in a fair die)=}(1)/(6)`

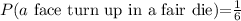
So,

`\begin{gathered} P(X_1)=(1)/(6);P(X_2)=(1)/(6);P(X_3)=(1)/(6) \\ P(X_4)=(1)/(6);P(X_5)=(1)/(6);P(X_6)=(1)/(6) \end{gathered}`

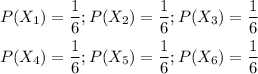
The expected sum of money the player can win is

`E(X)=n_1P(X_1)+n_2P(X_2)+n_3P(X_3)+n_4P(X_4)+n_5P(X_5)+n_6P(X_6)`
`\begin{gathered} n_1=n_3=n_5=0(\text{Given)} \\ n_2=\text{ \$20;} \\ n_4=\text{ \$40} \\ n_6=-\text{ \$30} \end{gathered}`
`E(X)=0((1)/(6))+20((1)/(6))+0((1)/(6))+40((1)/(6))+0((1)/(6))+(-30)((1)/(6))`
`\begin{gathered} E(X)=0+(20)/(6)+0+(40)/(6)+0-(30)/(6) \\ E(X)=(20+40-30)/(6) \\ E(X)=(60-30)/(6) \\ E(X)=(30)/(6) \\ E(X)=5 \end{gathered}`

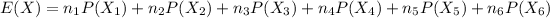
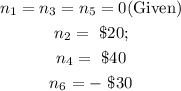
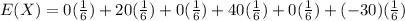
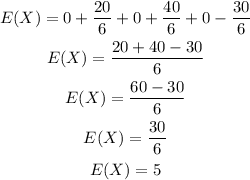
Hence, the expected sum of money the player can win is $5