(3,-2) is a solution to this system of inequalities.
1) A possible solution to a System of Inequalities is located on the common shaded region of both inequalities, on the graph.
2) Let's test algebraically and then locate it geometrically point (3,-2)
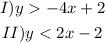
Let's plug into the first inequality the point (3,-2) and check:
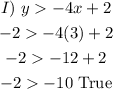
As we can see -2 is greater than -10. Now let's move on to test on the 2nd equation:
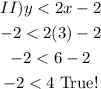
So, since point (3,-2) is true for both inequalities, and it is located in this region:
Note that the point belongs to both regions (red and blue).
3) Hence, (3,-2) is a solution to this system of inequalities.