Question

The function gx) = x is transformed to obtain function h.h(x) = g(x)-5.Which statement describes how the graph of his different from the graph of g?OA.The graph of h is the graph of g horizontally shifted left 5 units.The graph of h is the graph of gvertically shifted down 5 units.B.OC. The graph of h is the graph of g horizontally shifted right 5 units.OD.The graph of h is the graph of g vertically shifted up 5 units.

Answer 1

The parent function is

`g(x)=x^2`

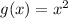
This function was transformed to obtain h(x), the transformation applied is represented by the following expression:

`h(x)=g(x)-5`

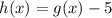
When you add/subtract a constant "k" from a function the type of transformation is a vertical translation.

For example, considering any function f(x)

-If you add "k" units to the function: f(x)+k, the resulting transformation will be a translation of "k" units up.

-If you subtract "k" units to the function: f(x)-k, the resulting transformation will be a translation of "k" units down.

With this in consideration, there were 5 units subtracted from g(x), which indicates that the function was shifted vertically 5 units down.

The correct option is B.