Step-by-step explanation:
Step 1: Obtain the system of linear equations that expresses the problem:
Let us denote by x the cost of each rose and by y the cost of each lily.
According to the problem, the first order is 1 rose and 6 lilies, the cost is 72 dollars:
This gives us the following linear equation:
Equation 1:
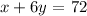
Now, the second order is:
2 roses and 3 lilies and the cost is 45 dollars.
This gives us the following linear equation:
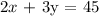
Step 2: write the system of linear equations:
Equation 1:
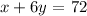
Equation 2:
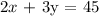 Step 3:
Step 3: Solve the system of linear equations by elimination method:
In the elimination method, you either add or subtract the equations to get an equation in one variable. When the coefficients of one variable are opposites you add the equations to eliminate a variable and when the coefficients of one variable are equal you subtract the equations to eliminate a variable.
In this case, we can subtract equation 1 twice from equation 2:
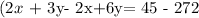
Applying the distributive property, this is equivalent to:
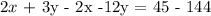
notice that now we can eliminate 2x from the above equation. Now this is equivalent to:
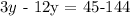
this is equivalent to:
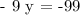
or
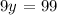
solving for y, we obtain:
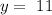
now, to find x, we can apply the above value to equation 1 and solve for x:
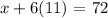
this is equivalent to:
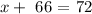
solving for x, we get:

we can conclude that the correct answer is:
Answer:
x = Cost of each rose = $6
y = Cost of each lily = $11