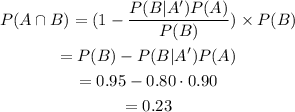Question

An investment firm is interested in the performance of it's accounting department's audit reports.Audit reports are classified based on two sets of criteria: On-time or Late submission and Complete or Incomplete. After some research, it has come up with the following information:The probability that an audit report is incomplete is 0.05The probability that an audit report is complete given it was submitted late is 0.80The probability that an audit report is on-time is 0.90What is the probability that the audit report is complete and not late?

Answer 1

On this problem, we have two sets of criteria. Let's call the event A as the event of the audit report to be on-time, consequently being late is the complement of A(noted as A'), and the event B as the event of the audit report to be

complete(incomplete reports noted as B').

From the text, we know that the probability that an audit report is incomplete is 0.05

`P(B^(\prime))=0.05`

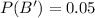
The probability that an audit report is complete given it was submitted late is 0.80

`P(B|A^(\prime))=0.80`

and the probability that an audit report is on-time is 0.90

`P(A)=0.90`

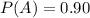
The probability of an event and its complement must add up to 1, because only one of them can happen. This gives to us the following probabilities

`\begin{gathered} P(A)=0.90\Rightarrow P(A^(\prime))=0.10 \\ P(B^(\prime))=0.05\Rightarrow P(B)=0.95 \end{gathered}`

We want to calculate the probability that the audit report is complete and not late

`P(A\cap B)`

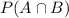
Using the conditional probability formula, this probability is given by

`P(A\cap B)=P(A|B)P(B)`

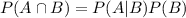
We already know the probability for B to happen, now we need to determinate the probability for A to happen given B. We already have the probability for B to happen given the A'. Using the Bayes Theorem we can calculate the probability of A' happening given B, and this will be the complement of P(A|B).

`P(A|B)+P(A^(\prime)|B)=1`

Calculating P(A'|B) using the Bayes Theorem, we have

`P(A^(\prime)|B)=(P(B|A^(\prime))P(A))/(P(B))`

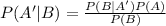
Then, P(A|B) is

`P(A|B)=1-(P(B|A^(\prime))P(A))/(P(B))`

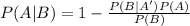
Then, the probability that the audit report is complete and not late is

`\begin{gathered} P(A\cap B)=(1-(P(B|A^(\prime))P(A))/(P(B)))* P(B) \\ =P(B)-P(B|A^(\prime))P(A) \\ =0.95-0.80\cdot0.90 \\ =0.23 \end{gathered}`