![\text{Given that }\Delta ABC\cong\Delta DEF]()
Let us take by SSS these triangles are congruent.
So these two triangles have equal corresponding angles.
![\angle ABC=\angle DEF]()
Consider the triangle GEC.
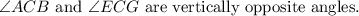
Recall that vertically opposite are always equal.

![\angle DEF\text{ and }\angle CEG\text{ are vertically opposite angles.}]()
![\angle DEF\text{ =}\angle CEG]()
![\text{ Replace that }\angle ABC=\angle DEF\text{ .}]()
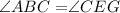
Hence triangles ABC and GEC have corresponding two angles that are equal.
If two corresponding angles are equal then third must be equal.
For example
By using the triangle sum property on triangle ABC, we get
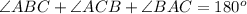
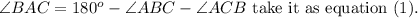
Similarly to triangle GEC.


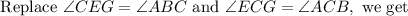
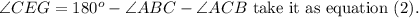
Comparing equations (1) and (2), we get that

Therefore triangles ABC and GEC are similar since their corresponding angles are congruent.