a) The sample mean is given by the formula below
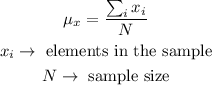
Therefore, in our case,
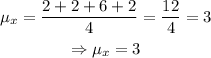
On the other hand, the sample standard deviation is
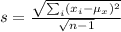
Thus, in the case of the given sample,
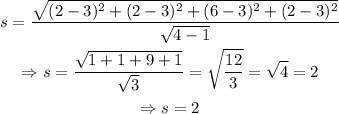
The sample mean is 3 and the sample standard deviation is 2.
b) The estimated standard error of the mean is given by the formula below
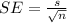
Hence, in our case,

The estimated standard error for the mean is equal to 1.