The North side is equal to the South side, as we have a rectangle for the field.
Then we can write:

With the value of x we can calculate all four sides:
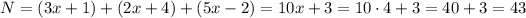
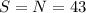
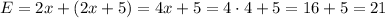
We know that West = East, but we will add it independently to verify it is correct:
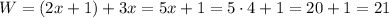
Answer:
North side = 43
South side = 43
East side = 21
West side = 21