Question

suppose we want to choose 2 colors without replacement from 5 colors red blue green purple yellow (a) how many ways can this be done if the order of choices matters?(b) how many ways can this be done if order does not matter?

Answer 1

Step-by-step explanation

Given:

Elements to choose from = 5

Elements chosen = 2

a)

To determine the number of ways it can be done if the order of choices matters, we use the formula below:

`_nP_r=(n!)/((n-k)!)`

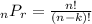
where:

n=elements to choose from

k=elements chosen

P=Permutation

We plug in what we know:

`\begin{gathered} _nP_k=(n!)/((n-k)!) \\ _5P_2=(5!)/((5-2)!) \\ Simplify \\ _5P_2=(5!)/(3!) \\ _5P_2=20 \end{gathered}`

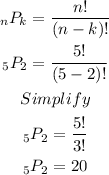
Hence, there are 20 ways this can be done if the order of choices matters and without replacement.

b)

To determine the number of ways this can be done if order does not matter, we use the formula:

`_nC_k=(n!)/(k!(n-k)!)`

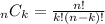
where:

n=elements to choose from

k=elements chosen

C=Combination

We plug in what we know:

`\begin{gathered} _(n)C_(k)=(n!)/(k!(n-k)!) \\ _5C_2=(5!)/(2!(5-2)!) \\ Simplify \\ _5C_2=(5!)/(2!(3!)) \\ _5C_2=10 \\ \end{gathered}`

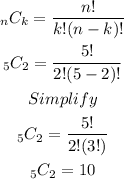
Hence, there are 10 ways that this can be done if order does not matter and without replacement.