Question

a beaker contains 150ml of 0.14 mol/L solution of strontium nitrate. if 350 mL of water is added to the beaker, what will be the concentration of strontium nitrate?

Answer 1

What remains constant before and after the addition of water is the number of moles in the beaker.

So, let the concentration be c₁ and c₂ (before and after), the number of moles be n and the volume before be V₁ and after be V₂.

The equation for concentration is number of moles divided by the volume, so we have, for before the addition:

`c_1=(n)/(V_1)\leftrightarrow n=c_1V_1`

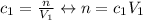
And the equation for after:

`c_2=(n)/(V_2)\leftrightarrow n=c_2V_2`

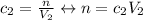
Notice that we didn't put subscripted number on n because this won't change.

Because n doesn't change, we can say:

`\begin{gathered} n=n \\ c_1V_1=c_2V_2 \\ c_2=(c_1V_1)/(V_2)_{}_{} \end{gathered}`

We know c₁ is 0.14 mol/L and V₁ is 150 mL.

The volume after the addition will be the volume before plus the amount we added, so:

`V_2=150+350=500`

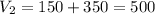
Thus, the final concentration will be:

`c_2=\frac{0.14mol/L\cdot150\cancel{mL}}{500\cancel{mL}}=0.042mol/L`

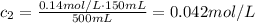
The final concentration will be 0.042 mol/L.