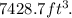Question

how much liquid can i fill the rectangular prism if i put the solid cyclinder inside? round to the nearest tenth.

Answer 1

To answer this question we will use the following formulas to compute the volume of a rectangular prism and a cylinder:

`\begin{gathered} V_(prism)=length* width* height, \\ V_(cylinder)=\pi* radius^2* height. \end{gathered}`

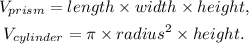
From the given diagram we get that the length of the rectangular prism is 24ft, its width is 16ft and its height is 20ft, therefore its volume is:

`V_(prism)=24ft*16ft*20ft=7680ft^3.`

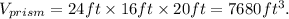
Also, from the given diagram we get that the radius of the cylinder is 4ft and its height is 20ft, therefore its volume is:

`V_(cylinder)=\pi*(4ft)^2*20ft=80\pi ft^3\approx251.3ft^3.`

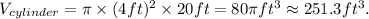
Then:

`7680ft^3-251.3ft^3=7428.7ft^3`

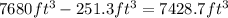
Answer:

`7428.7ft^3.`