EXPLANATION
Vertex:
The vertex of an up-down facing parabola of the form:

is:
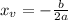
Rewrite
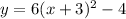
in the form y=ax^2 +bx + c
Expanding:
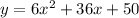
The parabola params are:
a=6, b=36, c=50
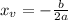

Simplify:
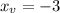
Plug in x_v = -3to find the y_v value
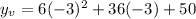
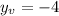
Therefore the parabola vertex is (-3,-4)
a=6 so the vertex is a minimum.
Axis:
Parabola standard equation
4p(y-k) = (x-h)^2 is the standard equation for an up-down facing parabola with vertex at (h,k), and a focal length p
Rewrite y=6(x+3)^2-4 in the standard form:
Add 4 to both sides
y + 4 = 6(x+3)^2 -4+4
Refine
y+4 = 6(x+3)^2
Divide both sides by 6
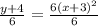
Simplify
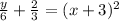
Factor 1/6
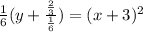
Simplify:

Factor 4:
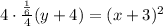
Simplify:
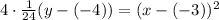
Therefore parabola properties are:
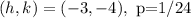
Parabola is of the form 4p(y-k)=(x-h)^2 and is symmetric around the y-axis.
Axis of symmetry is a line parallel to the y-axis wich intersects the vertex:
x = -3