To find the restricted values for a rational function we need to determine for which values of x the denominator is zero, this values are the restricted values. This comes from the fact that we can't divide by zero.
With this in mind, for the expression:
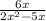
we need to find when:
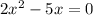
Solving this equation we have that:
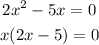
the last equivalent expression implies that:
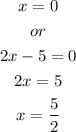
Therefore the restricted values of x are 0 and 5/2