The value of x - co-ordinate of point A is cos(2π/3)
Step - by - Step Explanation
Given that:
We know that if any unit circle which radius is r (r=1) and angle is θ then its coordinate will be:
x = rcos θ
y = r sinθ
In the figure given to us θ will be;
θ = π / 2 + π /6
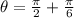
Simplify
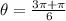
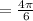
We can reduce the fraction above by 2.
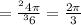
But the x - coordinate is given by :
x= rcos θ
From the figure, it is a unit circle, so r = 1
We've calculated θ = 2π /3
Substitute the values into x = rcosθ
x = 1 . cos (2π /3)
Therefore, the value of x- coordinate is cos(2π/3)