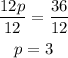Given the expression
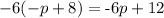
To solve this equation you have to solve the multiplication on the term of the left to get rid of the ( ), so that both sides are expressed in the same way.
To solve the parenthesis you have to apply the distributive property of multiplication:
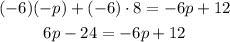
Now is time to rearrange the equation so that all terms related to the unknown value "p" stay in one side of the = sign and all other values stay in the other side.
To "pass" the term from one side to the other side, you have to perform the inverse operation, this is, if the number is being added, you have to subtract it.
For the equality to continue to be valid, every operation you do in one side of the equation has to be done in the other side, so:
24 is being subtracted in the equation, so the inverse operation will be to add it to both sides of the equation, on the right side the opposing operations will undo each other and it would seem as if it "passed" to the right side:
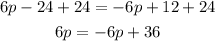
Next is to pass the term "6p" from the rigth side of the = sign to its left side. As before, to do so you have to perform the inverse operation in both sides of the equation to keep the equality.
"6p" is negative, so the inverse operation will be to add it to both sides of the equation:
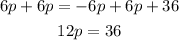
Finally you see that p is being multiplied by 12 and you need to know the value of p alone so to cancel this multiplication you have to perform the inverse operation, which is a division. And since you need to mantain the equality in both sides of the sign, you have to divide both sides by 12: