Question

Which two forces will cause the same rate of change in the stick's angular momentum as each other.

Answer 1

Given:

The stick is attached to a pivot at the right end.

The four forces are,

`40\text{ N, 60 N, 30 N, 150 N}`

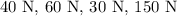
Any one of the forces can act on that stick at a time.

To find:

Which two forces will cause the same rate of change in the stick's angular momentum

Step-by-step explanation:

Let the length of each space be x.

To produce the same rate of change in angular momentum, the forces should produce the same torque.

The torque produces by the force,

`40\text{ N}`

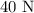
is,

`\begin{gathered} 40*4x\text{ \lparen the distance of this force from the right end is 4x\rparen} \\ =160x \end{gathered}`

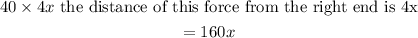
Similarly, the torque by 60 N force is,

`\begin{gathered} 60*3x \\ =180x \end{gathered}`

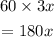
by 30 N force is,

`\begin{gathered} 30*2x \\ =60x \end{gathered}`

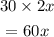
by 150 N force is,

`150x`

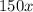
Here, we see all the torques are different from each other.

Hence, they all are different.