Question

Directions in pic. Number 15 and also when you graph it do the main function in red and inverse in blue

Answer 1

To find the inverse of a function, you have to start by replacing the f(x) by y:

`\begin{gathered} f(x)=-x^2+6 \\ y=-x^2+6 \end{gathered}`

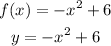
Now switch the x and y:

`x=-y^2+6`

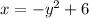
Solve for y:

`\begin{gathered} \text{Subtract 6 from both sides} \\ x-6=-y^2+6-6 \\ x-6=-y^2 \\ \text{ Multiply both sides by -1} \\ -1(x-6)=-1(-y^2) \\ 6-x=y^2 \\ \text{Apply square root to both sides} \\ \sqrt[]{6-x}=\sqrt[]{y^2} \\ \sqrt[]{6-x}=y \\ \text{Then,} \\ y=\sqrt[]{6-x} \end{gathered}`

Finally, replace y by f^-1(x):

`f^(-1)(x)=\sqrt[]{6-x}`

The graph of the main function is in red, and the graph of the inverse function is in blue:

As you can see, the graph of the inverse function (blue) is the graph of the main function (red) reflected about the diagonal line y=x (orange). Then, the inverse relationship is verified.